Design Modules in VisualDOC

VisualDOC can perform linear, non-linear, constrained and unconstrained, as well as integer, discrete and mixed optimization. The design modules in VisualDOC include: Gradient-based, Non-gradient-based, and Response Surface Optimization along with Design of Experiments and Probabilistic Analysis and Optimization. Multi-objective optimization is also available in VisualDOC. The details of each design module are as follows:

Optimization

Optimization_min.png

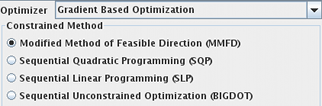
Optimization Property Editor

Direct Gradient-based Optimization (DGO)

VisualDOC calls DOT and BIGDOT to perform gradient-based optimization. The following optimization algorithms are included.

  • Modified Method of Feasible Direction (MMFD)
  • Sequential Linear Programming (SLP)
  • Sequential Quadratic Programming (SQP)
  • Sequential Unconstrained Optimization (BIGDOT)
  • Broydon Fletcher Goldfarb Shanno (BFGS)
  • Fletcher-Reeves (FR)

 Non-gradient based optimization (NGO)

VisualDOC includes state-of-the-art non-gradient based optimization methods. These methods attempt to emulate the natural phenomenon by modeling the optimization process such that it can be mapped to the entities of the natural process in an abstract sense. The following non-gradient-based optimization methods are included.

  • Particle swarm optimization (PSO)
  • Non-dominated Sorting Genetic Algorithm II (NSGAII)

 Multi-objective Optimization

In VisualDOC, the user can easily generate a Pareto-optimal (PO) front with NSGA-II or any other optimization method. To generate a PO front with single-objective optimization algorithms, scalarization using methods such as weighted-sum, ε-constraint, or compromise programming can be performed, and VisualDOC systematically varies the weight/ε-value/targets to generate the entire PO front

Design of Experiments (DOE)

With Design of Experiments module, the user can create an experimental design, construct the response surface model for this design, and analyze the characteristics of the design and the approximate model. The user can also use the generated approximate model optimization or other tasks.

doescattermatrix_min.png

A DOE Sample

The list of available DOE design methods is as follows.

  • Factorial Design
  • Central Composite Design
  • Box-Behnken Design
  • Koshal Design
  • Standard Latin Hypercube and Optimal Latin Hypercube Design
  • Taguchi Design
  • Simplex Design
  • Random Design
  • User Defined
  • D-Optimal Design

The approximation models consist of:

  • Linear
  • Mixed: Linear + Interaction
  • Mixed: Linear + Quadratic
  • Full Quadratic
  • Forward Stepwise Regression

Response Surface Approximate Optimization (RSA)

approx.png

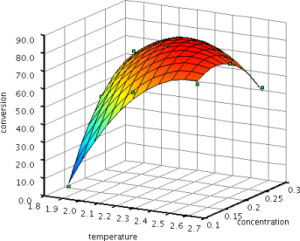
An Approximate Surface

The RSA component combines Optimization (OPT), Design of Experiments (DOE), and Response Surface Modeling (RSM) to improve optimization efficiency. The approximation is used as a surrogate for the underlying computationally expensive analyses and is incrementally refined as the optimization proceeds. The user can choose the DOE technique, the optimization algorithm, and the approximation model to use with the RSA component.

The following approximation models are available:

  • Linear
  • Mixed: Linear + Interaction
  • Mixed: Linear + Quadratic
  • Full Quadratic
  • Forward Stepwise Regression
error while rendering dynamore.policy.portlet-tiles